My Profile Photo

Mucio Osorio

Blog del curso de Probabilidad y Estadística

Estadística descriptiva

ESTADISTICA DESCRIPTIVA. LAS SEIS CARACTERÍSTICAS DE LOS DATOS

En estas notas se estudian las herramientas estadísticas esenciales en el análisis descriptivo de los datos y que estan basadas en el artículo “The Six Characteristics of a Dataset”. Para ejecutar un pedazo de código (Chunk) solo dar “clic” en el boton verde de Ejecutar (Run) o situando el cursor en la linea a ejecutar y presionar Ctrl+Shift+Enter.

En el proceso Estadístico, una vez que se han conseguido los datos lo primero que tendremos que hacer es analizarlos de diferentes maneras. Las siguientes seis características son un buen punto de partida.

The Old Faithful Dataset

Geyser Old Faithful

Geyser Old Faithful

El conjunto de datos del geyser “Old Faithful” consta de 272 medidas de la duración de la exhalación (min) del geyser y del tiempo entre exhalaciones (min). Puede accederse a ellos desde R solo escribiendo en la consola faithful y ejecutando dicha instrucción. Tiene características interesantes que servirán para ejemplificar las herramientas de la Estadística Descriptiva.
x = faithful
eyJsYW5ndWFnZSI6InIiLCJzYW1wbGUiOiJmYWl0aGZ1bCAgICAgICJ9

Si se requiere Información sobre los datos old faithful solo escriba ?faithful

## starting httpd help server ... done

1. Localización de los datos.

Con éstas medidas se pretende tener una idea de la ubicación de los datos en algún lugar de los números reales. Es importante dar la posición del dato más pequeño, del dato más grande, de lo que en Estadística se conoce como la tendencia central de los datos y los cuantiles (que dan otras ubicaciones incluidas las centrales).

En R, éstas medidas pueden obtenerse de diversas maneras a través de los distintoss paquetes, ya sea de manera individual o como parte de un resumen. En este trabajo se usan solo paquetes del sistema base de R y en el caso de que se use algún otro paquete se instalará para su uso.

  1. Mínimo. Es el valor más pequeño de los datos, si se encuentran ordenados es muy fácil ubicarlo.
    El tiempo mínimo que tarda una erupción es 1.6 minutos.

    eyJsYW5ndWFnZSI6InIiLCJzYW1wbGUiOiJtaW4oZmFpdGhmdWwkZXJ1cHRpb25zKVxubWluKGZhaXRoZnVsJHdhaXRpbmcpIn0=

  2. Máximo. El valor más grande de los datos.

    eyJsYW5ndWFnZSI6InIiLCJzYW1wbGUiOiJtYXgoZmFpdGhmdWwkZXJ1cHRpb25zKVxubWF4KGZhaXRoZnVsJHdhaXRpbmcpIn0=

  3. Tendencia central

     3.1 Moda

    Es el dato que más veces aparece

    eyJsYW5ndWFnZSI6InIiLCJzYW1wbGUiOiJ0YWJsZShmYWl0aGZ1bCRlcnVwdGlvbnMpXG50YWJsZShmYWl0aGZ1bCR3YWl0aW5nKSJ9 
     3.2 Mediana

    La mediana corresponde al dato que se ubica justo a la mitad, cuando se ordenan

    eyJsYW5ndWFnZSI6InIiLCJzYW1wbGUiOiJtZWRpYW4oZmFpdGhmdWwkZXJ1cHRpb25zKVxubWVkaWFuKGZhaXRoZnVsJHdhaXRpbmcpIn0= 
     3.3 Media

La media aritmética es la medida de tendencia central más conocida. La mayor parte de la gente la llama el promedio. En una muestra el símbolo de la estadística de la media es \[\overline{x}\] y corresponde a la suma de todas las observaciones dividida por el número de observaciones \[\frac{\sum_{i=1}^{n}{x_i}} {n}\] .

eyJsYW5ndWFnZSI6InIiLCJzYW1wbGUiOiJtZWFuKGZhaXRoZnVsJGVydXB0aW9ucylcbm1lYW4oZmFpdGhmdWwkd2FpdGluZykifQ==
  1. Cuantiles. La palabra cuantil viene de la palabra cantidad. En terminos simples, un cuantil es cuando se divide al conjunto de datos en subgrupos adyascentes de igual tamaño. Especificamente, los cuantiles reciben diferentes nombres en función de la cantidad de partes enque se divide a los datos. Por ejemplo cuando se divide a los datos en 100 partes iguales, los cuantiles se denominan percentiles y se identifican con la notación Pj (con 0<j<1) y cuando la división es en 4 partes se llaman Cuartiles y se identifican con Qk (k=1,2,3)
    eyJsYW5ndWFnZSI6InIiLCJzYW1wbGUiOiJxdWFudGlsZShmYWl0aGZ1bCRlcnVwdGlvbnMpXG5xdWFudGlsZShmYWl0aGZ1bCR3YWl0aW5nKVxuIyBTaSBzZXJlcXVpZXJlIHNvbG8gdW4gY3VhbnRpbCAocG9yIGVqZW1wbG8gZWwgMTAlKVxucXVhbnRpbGUoZmFpdGhmdWwkZXJ1cHRpb25zLDAuMTApIFxuIyBzaSBzZXJlcXVpZXJlIG1cdTAwZTFzIGRlIHVuIGN1YW50aWwsIGRvbmRlIGMoMC4xMCwwLjQ1LDAuOTkpIGVzIHVuIHZlY3RvciBkZSBjdWFudGlsZXMgYSAgY2FsY3VsYXJcbnF1YW50aWxlKGZhaXRoZnVsJHdhaXRpbmcsYygwLjEwLDAuNDUsMC45OSkpICJ9
    Para calcular los percentiles existen varios métodos. En R, use el tipo 2 para obtener los mismos resultados que los obtenidos en clase.
    eyJsYW5ndWFnZSI6InIiLCJzYW1wbGUiOiJxdWFudGlsZShmYWl0aGZ1bCRlcnVwdGlvbnMsIHR5cGUgPSAyKVxucXVhbnRpbGUoZmFpdGhmdWwkd2FpdGluZywgdHlwZSA9IDIpIn0=

Dispersión o variabilidad

Estudia la distribución de los valores de la serie, analizando si estos se encuentran más o menos concentrados, o más o menos dispersos. Existen diversas medidas de dispersión, entre las más utilizadas podemos destacar las siguientes:

  • Amplitud.
Es la medida de dispersión más fácil de obtener. Se obtiene hallando la diferencia entre la observación mayor y la menor (el valor máximo menos el valor mínimo). La amplitud es una medida muy influenciada por los valores extremos y por lo tanto puede dar una impresión falsa sobre los valores reales de la distribución.
eyJsYW5ndWFnZSI6InIiLCJzYW1wbGUiOiJyYW5nZShmYWl0aGZ1bCRlcnVwdGlvbnMpXG5yYW5nZShmYWl0aGZ1bCR3YWl0aW5nKSJ9

En R, la función diff cálcula la diferencia de dos cantidades:

eyJsYW5ndWFnZSI6InIiLCJzYW1wbGUiOiJkaWZmKHJhbmdlKGZhaXRoZnVsJGVydXB0aW9ucykpXG5kaWZmKHJhbmdlKGZhaXRoZnVsJHdhaXRpbmcpKSJ9
  • Varianza.

Mide la distancia (cuadrada) existente entre los valores de la serie y la media. Mientras más se aproxima a cero, más concentrados están los valores de la serie alrededor de la media. Por el contrario, mientras mayor sea la varianza, más dispersos están. El símbolo para representar a la varianza muestral es \[{s^2}\] y para la varianza poblacional \[{\sigma ^2}\].

\[s^2=\frac{\sum_{i=1}^{n}\left(x_i-\bar{x}\right)^2}{n-1}\]

\[\sigma^2=\frac{\sum_{i=1}^{N}\left(x_i-\mu\right)^2}{N}\]
eyJsYW5ndWFnZSI6InIiLCJzYW1wbGUiOiJ2YXIoZmFpdGhmdWwkZXJ1cHRpb25zKVxudmFyKGZhaXRoZnVsJHdhaXRpbmcpIn0=
  • Desviación estándar o típica.
Se calcula como raíz cuadrada de la varianza.
eyJsYW5ndWFnZSI6InIiLCJzYW1wbGUiOiJzZChmYWl0aGZ1bCRlcnVwdGlvbnMpXG5zZChmYWl0aGZ1bCR3YWl0aW5nKSJ9

Nótese que ni la varianza ni la desviación estándar pueden ser negativas y son cero sólo cuando todos los datos tienen el mismo valor que no es otro que el valor de la media.

Valores extremos.

Los diagramas de Caja-Bigotes (boxplots o box and whiskers) son una presentación visual que describe varias características importantes, al mismo tiempo, tales como la dispersión, la tendencia central y simetría. Tambien se usa para detectar valores atípicos (extremos).

Para su realización se representan en una caja o rectángulo los tres cuartiles (\(P_{0.25}\), \(P_{0.50}\) y \(P_{0.75}\)) y se trazan lineas hasta máximo una distancia de 1.5(P0.75-P0.25). De modo que cualquier dato o caso que no se encuentre dentro de este rango es identificado como un valor extremo.

eyJsYW5ndWFnZSI6InIiLCJzYW1wbGUiOiJib3hwbG90KGZhaXRoZnVsJGVydXB0aW9ucylcbmJveHBsb3QoZmFpdGhmdWwkd2FpdGluZykifQ==

4. Forma de los datos o distribución de frecuencias.

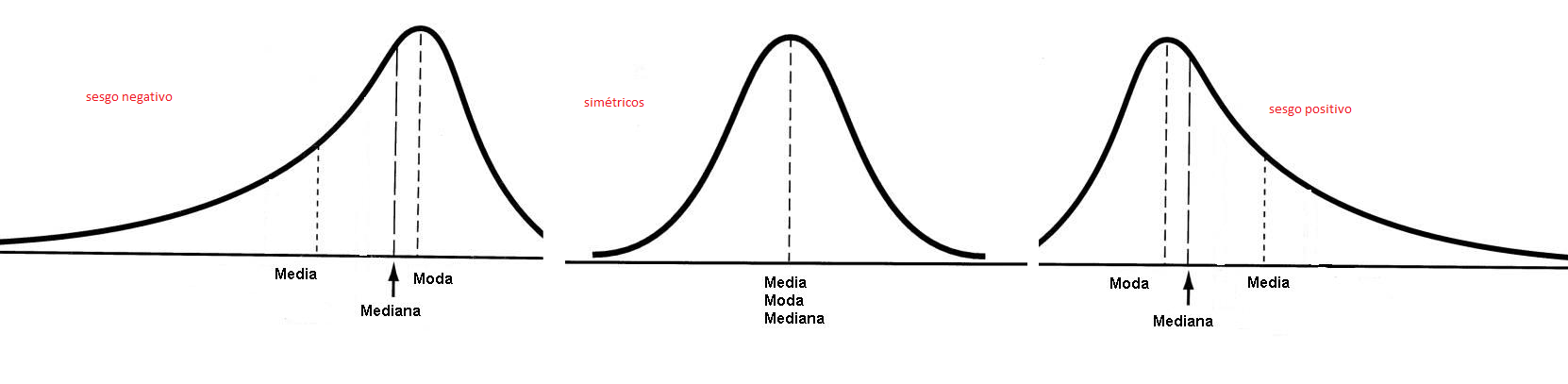
La distribución de frecuencias es el principal factor en la determinación de las medidas que mejor describen a los datos. Así que debería ser la primera característica a revisar. Normalmente, se concluye que los datos son simétricos o asimétricos (con sesgo positivo o negativo) o tambien se clasifica a los datos como unimodales, bimodales o multimodales.

Una herramienta útil para visualizar la forma de los datos es el histograma.

eyJsYW5ndWFnZSI6InIiLCJzYW1wbGUiOiJwYXIobWZjb2w9YygxLDIpKVxuaGlzdChmYWl0aGZ1bCRlcnVwdGlvbnMpXG5oaXN0KGZhaXRoZnVsJHdhaXRpbmcpIn0=

La relación entre la gráfica de la distribución y las medidas de tendencia central.

  • En distribuciones unimodales cuando la media, la moda y la mediana coinciden la distribución es simétrica.

  • En distribuciones unimodales cuando la media, la moda y la mediana no coinciden la distribución es sesgada.Si la media es mayor que la mediana (la media a la derecha de la mediana) entonces la distribución está sesgada a la derecha (o positivamente).

  • Si la media es menor que la mediana (la media a la izquierda de la mediana) entonces la distribución está sesgada a la izquierda (o negativamente)

5. Agrupamientos o clústers

La agrupación implica que los datos tienden a acumularse alrededor de ciertos valores, por ejemplo, los salarios anuales de una empresa pueden agrupars alrededor de 5000 pesos para trabajadores no calificados, 10000 pesos para trabajadores calificados y 15000 pesos para los administrativos. Los agrupamientos pueden detectarse en un histograma o un gráfico de puntos.

eyJsYW5ndWFnZSI6InIiLCJzYW1wbGUiOiJwbG90KGZhaXRoZnVsJGVydXB0aW9ucylcbmhpc3QoZmFpdGhmdWwkZXJ1cHRpb25zKSJ9

6. Correlación

La correlación indica la fuerza y la dirección de una relación lineal entre dos variables. Se considera que dos variables cuantitativas están correlacionadas cuando los valores de una de ellas varían sistemáticamente con respecto a los valores de la otra: si tenemos dos variables (A y B) existe correlación positiva entre ellas si al disminuir los valores de A lo hacen también los de B y viceversa y tenemos una relación negativa si al disminuir los valores de A aumentanlos de B o viceversa. La correlación entre dos variables no implica, por sí misma, ninguna relación de causalidad.

correlacion

correlacion

La herramienta que sirve para visualizar la relación entre dos variables se llama diagrama de dispersión

eyJsYW5ndWFnZSI6InIiLCJzYW1wbGUiOiJwbG90KGZhaXRoZnVsJHdhaXRpbmcsZmFpdGhmdWwkZXJ1cHRpb25zKSJ9

El coeficiente de correlación de Pearson es una cantidad que mide la correlación entre variables.

\[ r = \frac{n \sum{XY}-(\sum{X}\sum{Y})}{\sqrt{ [n \sum{x^2}-(\sum{x})^2 ][n \sum{y^2}-(\sum{y})^2 }]} \]

eyJsYW5ndWFnZSI6InIiLCJzYW1wbGUiOiJjb3IoZmFpdGhmdWwkZXJ1cHRpb25zLGZhaXRoZnVsJHdhaXRpbmcpIn0=
eyJsYW5ndWFnZSI6InIiLCJzYW1wbGUiOiJsYXlvdXQobWF0cml4KGMoMSwyLDMsMyksIDIsIDIsIGJ5cm93ID0gVFJVRSkpXG5ib3hwbG90KGZhaXRoZnVsJGVydXB0aW9ucylcbmJveHBsb3QoZmFpdGhmdWwkd2FpdGluZylcbmhpc3QoZmFpdGhmdWwkd2FpdGluZykifQ==

Material de apoyo

  1. Cálculo de medidas de tendencia central y de variabilidad. http://mucioosorio.github.io/probabilidad/doc/tendencia_central_variabilidad.pdf

  2. Construcción de histograma. http://mucioosorio.github.io/probabilidad/doc/Histograma.pdf

Cuarteto de Anscombe

https://es.wikipedia.org/wiki/Cuarteto_de_Anscombe

El cuarteto de Anscombe comprende cuatro conjuntos de datos que tienen las mismas propiedades estadísticas, pero que evidentemente son distintas al inspeccionar sus gráficos respectivos.

Cada conjunto consiste de once puntos (x, y) y fueron construidos por el estadístico F. J. Anscombe. El cuarteto es una demostración de la importancia de mirar gráficamente un conjunto de datos antes de analizarlos.

Para los cuatro conjuntos de datos:

I II
x y x y
10.0 8.04 10.0 9.14
8.0 6.95 8.0 8.14
13.0 7.58 13.0 8.74
9.0 8.81 9.0 8.77
11.0 8.33 11.0 9.26
14.0 9.96 14.0 8.10
6.0 7.24 6.0 6.13
4.0 4.26 4.0 3.10
12.0 10.84 12.0 9.13
7.0 4.82 7.0 7.26
5.0 5.68 5.0 4.74

Realice un análisis de los 4 conjuntos de datos de Ascombe.

boxplot(faithful$waiting) ``` ## 4. Forma de los datos o distribución de frecuencias La distribución de frecuencias es el principal factor en la determinación de las medidas que mejor describen a los datos. Así que debería ser la primera característica a revisar. Normalmente, se concluye que los datos son **simétricos** o **asimétricos** (con sesgo positivo o negativo) o tambien se clasifica a los datos como **unimodales**, **bimodales** o **multimodales**. Una herramienta útil para visualizar la forma de los datos es el histograma. ```R par(mfcol=c(1,2)) hist(faithful$eruptions) hist(faithful$waiting) ``` ## La relación entre la gráfica de la distribución y las medidas de tendencia central. * En distribuciones unimodales cuando la media, la moda y la mediana coinciden la distribución es simétrica. * En distribuciones unimodales cuando la media, la moda y la mediana no coinciden la distribución es sesgada.Si la media es mayor que la mediana (la media a la derecha de la mediana) entonces la distribución está sesgada a la derecha (o positivamente). * Si la media es menor que la mediana (la media a la izquierda de la mediana) entonces la distribución está sesgada a la izquierda (o negativamente) ![forma-datos](/probabilidad/figs/06_forma-datos.png) ## 5. Agrupamientos o clústers La agrupación implica que los datos tienden a acumularse alrededor de ciertos valores, por ejemplo, los salarios anuales de una empresa pueden agrupars alrededor de 5000 pesos para trabajadores no calificados, 10000 pesos para trabajadores calificados y 15000 pesos para los administrativos. Los agrupamientos pueden detectarse en un histograma o un gráfico de puntos. ```R plot(faithful$eruptions) hist(faithful$eruptions) ``` ## 6. Correlación La correlación indica la fuerza y la dirección de una relación lineal entre dos variables. Se considera que dos variables cuantitativas están correlacionadas cuando los valores de una de ellas varían sistemáticamente con respecto a los valores de la otra: si tenemos dos variables (A y B) existe correlación positiva entre ellas si al disminuir los valores de A lo hacen también los de B y viceversa y tenemos una relación negativa si al disminuir los valores de A aumentanlos de B o viceversa. La correlación entre dos variables no implica, por sí misma, ninguna relación de causalidad. ![correlacion](/probabilidad/figs/07_correlacion.PNG) La herramienta que sirve para visualizar la relación entre dos variables se llama **diagrama de dispersión** ```R plot(faithful$waiting,faithful$eruptions) ``` El coeficiente de correlación de Pearson es una cantidad que mide la correlación entre variables. $$ r = \frac{n \sum{XY}-(\sum{X}\sum{Y})}{\sqrt{ [n \sum{x^2}-(\sum{x})^2 ][n \sum{y^2}-(\sum{y})^2 }]} $$ ```R cor(faithful$eruptions,faithful$waiting) ``` ```R layout(matrix(c(1,2,3,3), 2, 2, byrow = TRUE)) boxplot(faithful$eruptions) boxplot(faithful$waiting) hist(faithful$waiting) ``` ## Material de apoyo 1. Cálculo de medidas de tendencia central y de variabilidad. http://mucioosorio.github.io/probabilidad/doc/tendencia_central_variabilidad.pdf 2. Construcción de histograma. http://mucioosorio.github.io/probabilidad/doc/Histograma.pdf ## Cuarteto de Anscombe https://es.wikipedia.org/wiki/Cuarteto_de_Anscombe El cuarteto de Anscombe comprende cuatro conjuntos de datos que tienen las mismas propiedades estadísticas, pero que evidentemente son distintas al inspeccionar sus gráficos respectivos. Cada conjunto consiste de once puntos (x, y) y fueron construidos por el estadístico F. J. Anscombe. El cuarteto es una demostración de la importancia de mirar gráficamente un conjunto de datos antes de analizarlos. Para los cuatro conjuntos de datos: |I||II||III||IV| |--|--|--|--| |x|y|x|y|x|y|x|y| |10.0|8.04|10.0|9.14|10.0|7.46|8.0|6.58| |8.0|6.95|8.0|8.14|8.0|6.77|8.0|5.76| |13.0|7.58|13.0|8.74|13.0|12.74|8.0|7.71| |9.0|8.81|9.0|8.77|9.0|7.11|8.0|8.84| |11.0|8.33|11.0|9.26|11.0|7.81|8.0|8.47| |14.0|9.96|14.0|8.10|14.0|8.84|8.0|7.04| |6.0|7.24|6.0|6.13|6.0|6.08|8.0|5.25| |4.0|4.26|4.0|3.10|4.0|5.39|19.0|12.50| |12.0|10.84|12.0|9.13|12.0|8.15|8.0|5.56| |7.0|4.82|7.0|7.26|7.0|6.42|8.0|7.91| |5.0|5.68|5.0|4.74|5.0|5.73|8.0|6.89| Realice un análisis de los 4 conjuntos de datos de Ascombe.