Regresión Lineal Simple
Un modelo de regresión es un modelo que permite describir cómo influye una variable X sobre otra variable Y.
-
X: Variable independiente o explicativa o exógena o predictora
-
Y: Variable dependiente o respuesta o endógena
El objetivo es obtener estimaciones razonables de Y para distintos valores de X a partir de una muestra de n pares de valores \((x_1, y_1), (x_2,y_2),. . . ,(x_n, y_n)\).
Ejemplos
-
Estudiar cómo influye la estatura del padre (X) sobre la estatura del hijo (Y).
-
Estimar el precio de una vivienda (Y) en función de su superficie (X).
-
Aproximar la calificación obtenida en una materia (Y) según el número de horas de estudio semanal (X).
-
Prever el tiempo de cálculo de un programa (Y) en función de la velocidad del procesador (X).
-
Predecir la duración de una leche en días (Y) a partir de la temperatura a la que se almacena (X).
Supongamos que queremos encontrar la relación que hay entre las estaturas (X) y pesos (Y) de alumnos universitarios y que se consiguen las siguientes mediciones en 8 alumnos:
| Estatura (X) | Peso (Y) |
|---|---|
| 1.58 | 60 |
| 1.63 | 64 |
| 1.68 | 69 |
| 1.74 | 75 |
| 1.78 | 80 |
| 1.85 | 84 |
| 1.90 | 91 |
| 1.94 | 95 |
Para encontrar el modelo lo que se debe hacer es:
1.Ver la forma que tiene la relación entre las variables. Esto se consigue a través de un gráfico de dispersión
En éste puede verse que la forma de la relación es cómo un línea recta. Pero no solo puede haber relaciones lineales:
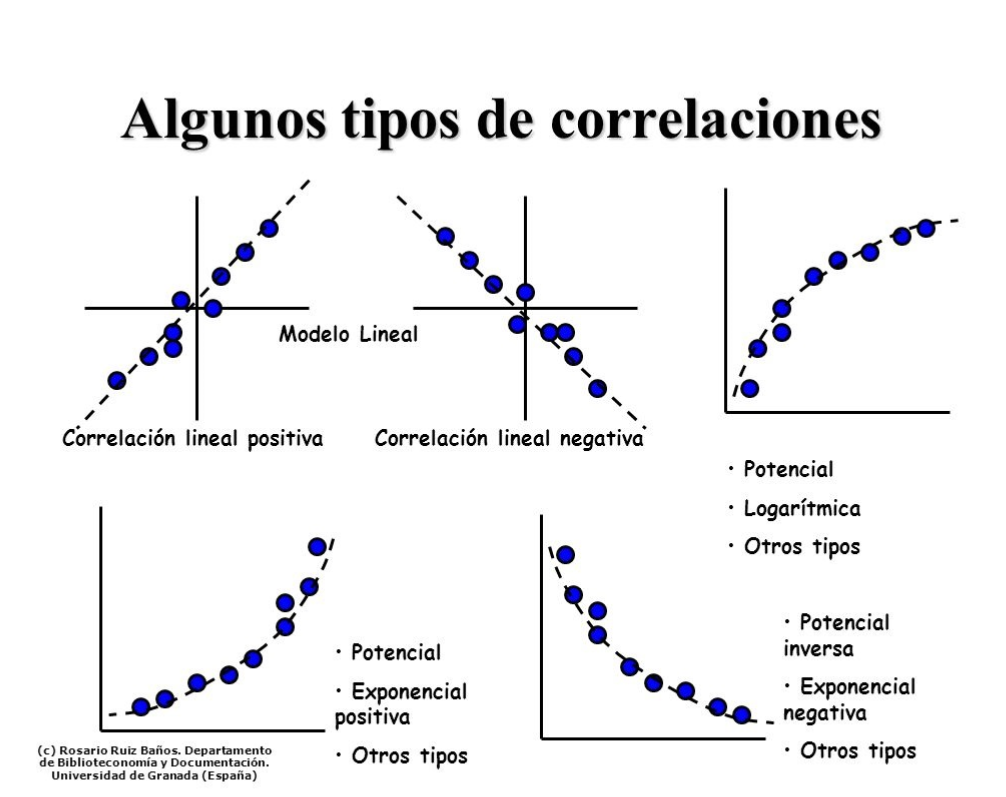
2.Se debe describir el sentido y la fuerza de la relación.
Sentido de la relación
-
Puede ser positivo, si cuando X crece tambien lo hace Y o viceversa. En este caso el coeficiente de correlación es positivo.
-
Negativo, si Y disminuye cuando X crece.El coeficiente de correlación es negativo.
Las estaturas y los pesos se relacionan con sentido positivo, pues si crece l estatura también lo hace el peso.
Fuerza de la relación
Tiene que ver con lo cercano que están los puntos originales a una linea (ya sea recta o curva) imaginaria que pasa entre los puntos.
En este caso puede decirse que hay una relación fuerte.
Dado que es subjetivo hablar sobre la fuerza de la relación sólo con ver el gráfico, hay un número que mide esa relación. Este número es el coeficiente de correlación de Pearson:
\[r = \frac{n \sum{XY}-(\sum{X}\sum{Y})}{\sqrt{ [n \sum{x^2}-(\sum{x})^2 ][n \sum{y^2}-(\sum{y})^2 }]}\]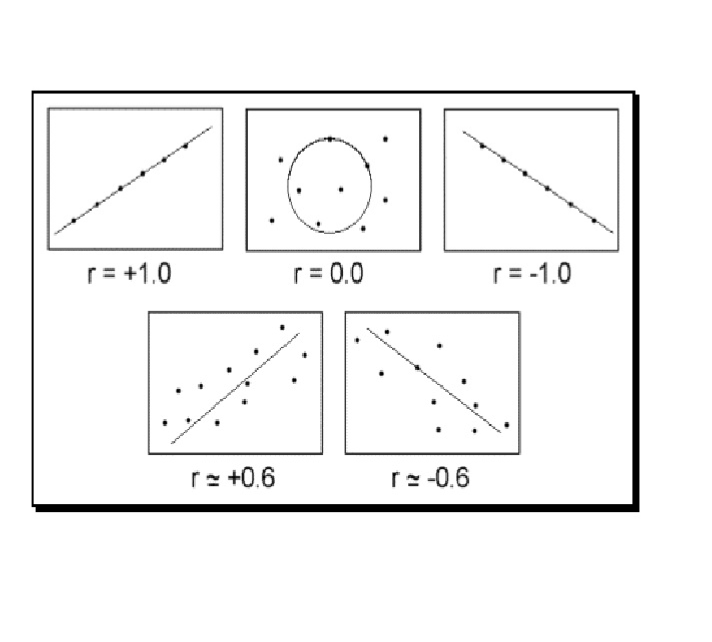
Los cálculos que deben hacersese muestran en la siguiente imágen:
Por lo que el coeficiente r es:
\[r = \frac{8* 1100.54-(14.1*618)}{\sqrt{ [8* 24.9678-14.1^2 ][8*48844-618^2 }]}=0.99772821\]esto quiere decir que hay una relación muy alta según la siguiente tabla (considere el valor absoluto).
3.cómo la forma de la relación es una linea recta, entonces habrá que calcular los parámetros de la linea recta que mejor representa esta relación:
\[Y = a + bX\]Donde a es la ordenada al origen y b es la pendiente de la recta. Para encontrar estos parámetros se recurre a un procedimiento denominado método de los mínimos cuadrados. Esto es, la línea recta obtenida con éste método pasa lo más cerca posiblede los pares de puntos:
\[b = \frac{n \sum{XY}-(\sum{X}\sum{Y})}{ n \sum{x^2}-(\sum{x})^2 }\] \[b= \frac{8* 1100.54-(14.1*618)}{ 8* 24.9678-14.1^2 }=97.08\]y la ordenada al origen
\[a = \bar{y}-b*\bar{x}\] \[a = \frac{618}{8}-97.08*\frac{14.1}{8}=-93.8535\]Finalmente, la ecuación de la linea recta es:
\[Y=-93.86+97.08*X\]Esta ecuación permite hacer estimaciones del peso de un alumno en fnción de su estatura, por ejemplo, si un alumno mide 1.73 ¿cuánto pesará?
Basta con sustituir en la ecuación para obteer el resultado de la estimación:
\[Y=-93.86+97.08*1.73=74.0949\]Es decir, que se espera que ese alumno pese aproximadamente 74.09 kg.
###TAREA
1.Los siguientes datos son sobre el tiempo en minutos de llamadas y el costo en pesos del servicio.
| Tiempo de llamada | Costo servicio |
|---|---|
| 2 | 2 |
| 4 | 5 |
| 6 | 7 |
| 8 | 9 |
| 10 | 11 |
-
¿Cuál es la variable que depende Y?
-
¿Cuál es la variable independiente X?
-
Construya el diagrama de dispersión. Diga cuál es la forma de la relación, cuál es el sentido
-
Calcule el coeficiente de correlación y haga la interpretación según la tabla.
-
Encuentre el valor de la pendiente b
-
Encuentre el valor de la ordenada al origen a
-
Escriba la ecuación que relaciona a estas dos variables.
-
Use esta ecuación para pronosticar cuánto costará una llamada que tarda 3.5 min
2.La duración de la leche en dias se relaciona con la temperatura de su almacenamiento en gradoscentígrados. Se obtuvieron los siguientes datos:
| Temperatura (centígrados) | Duración (días) |
|---|---|
| 0 | 24 |
| 5 | 20 |
| 10 | 16 |
| 15 | 10 |
| 20 | 2 |
| 25 | 1 |
-
¿Cuál es la variable que depende Y?
-
¿Cuál es la variable independiente X?
-
Construya el diagrama de dispersión.Diga cuál es la forma de la relación, cuál es el sentido
-
Calcule el coeficiente de correlación y haga la interpretación según la tabla.
-
Encuentre el valor de la pendiente b
-
Encuentre el valor de la ordenada al origen a
-
Escriba la ecuación que relaciona a estas dos variables.
-
Use esta ecuación para pronosticar cuánto durará la leche si se almacena a 3 grados centígrados
Asignación para entregar como máximo mañana viernes 15 de mayo.
Tareas que se reciban 1 día despues contarán 50%
Tareas que se reciban 2 días despues contarán 25%
Despues de dos diás solo contarán el 10%
Aquí: https://forms.gle/hYqRzywFzYVkd297A
Dudas se atienden en el correo mucio.osorio@itson.edu.mx Estoy atendiendolas lo mas pronto posible.
